|
EN BREF
|
Le calcul du volume d’un triangle rectangle peut paraître déroutant au premier abord, mais en comprenant les principes de base, il devient accessible à tous. En effet, un triangle rectangulaire ne peut pas être directement associé à un volume, car il s’agit d’une figure bidimensionnelle. Cependant, si l’on considère un prisme triangulaire dont la base est un triangle rectangle, le volume peut être calculé en multipliant l’aire de la base par la hauteur du prisme. Cette méthode ne se limite pas seulement à des tâches académiques, mais trouve également des applications pratiques dans de nombreux domaines tels que l’architecture, l’ingénierie et même la conception de produits. Pour explorer ce concept, il est essentiel de maîtriser les formules qui régissent l’aire d’un triangle rectangle avant d’aborder le volume d’un prisme triangulaire qui lui est associé.
Dans le domaine de la géométrie, le volume d’un triangle rectangle peut sembler déroutant. Cependant, sa détermination repose sur des principes simples. Cet article a pour objectif d’explorer la méthode de calcul du volume d’un triangle rectangle, en clarifiant les concepts d’aire et de hauteur, tout en illustrant des applications pratiques de ce calcul dans divers contextes.
Comprendre la notion de volume
Le volume représente l’espace occupé à l’intérieur d’un solide. Dans le cas d’un triangle rectangle, il s’agit de la partie d’un prisme triangulaire dont la base est formée par le triangle rectangle. Pour déterminer le volume, il convient de connaître l’aire de la base ainsi que la hauteur du prisme.
Calculer l’aire d’un triangle rectangle
Avant de passer au volume d’un triangle rectangle, il est fondamental de savoir comment calculer son aire. La formule simplifiée est la suivante :
A = (b × h) / 2
Dans cette formule, b représente la longueur de la base, et h celle de la hauteur (les deux côtés adjacents formant l’angle droit du triangle). Par exemple, si la base mesure 14 cm et la hauteur 28 cm, on obtient :
A = (14 × 28) / 2 = 196 cm²
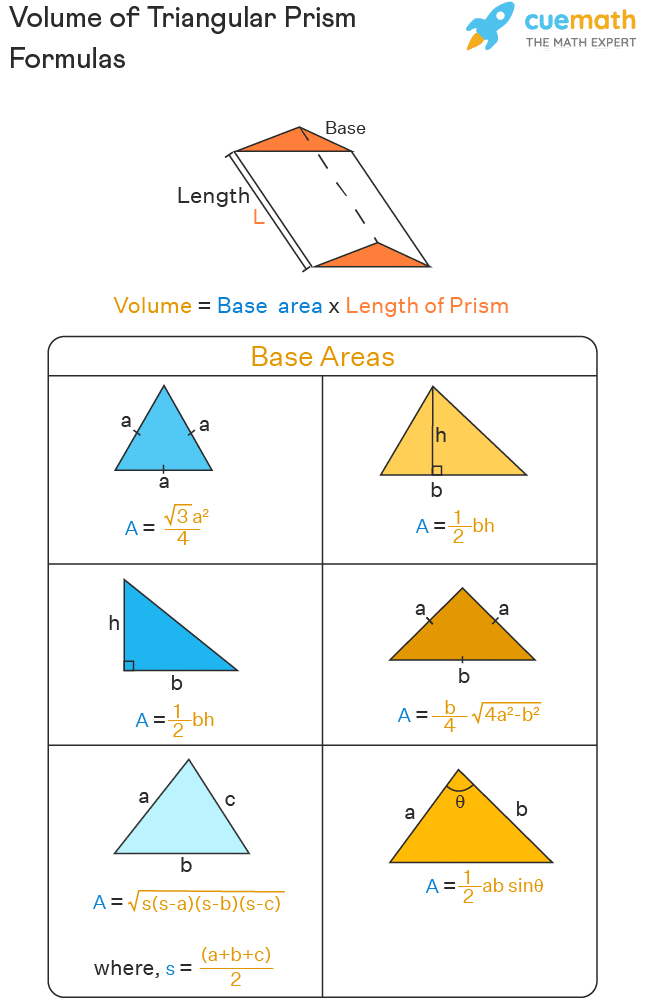
Formule pour le volume d’un prisme triangulaire
Pour obtenir le volume d’un prisme triangulaire dont la base est un triangle rectangle, nous utilisons la formule :
V = A × h
Ici, A est l’aire de la base (calculée précédemment), et h est la hauteur du prisme. Par exemple, si la base est de 196 cm² et la hauteur du prisme mesure 10 cm, alors :
V = 196 × 10 = 1960 cm³
Applications pratiques du volume d’un triangle rectangle
Comprendre le volume d’un triangle rectangle est crucial dans plusieurs domaines, notamment l’architecture et l’ingénierie. Les architectes, par exemple, doivent souvent calculer le volume des espaces pour concevoir des bâtiments et maximiser l’usage de l’espace. De plus, des situations du quotidien, comme la création de cupcakes sans moule, nécessitent aussi des connaissances en volume pour déterminer la capacité des contenants.
Démonstration d’un triangle rectangle
Pour prouver qu’un triangle est rectangle, on utilise le théorème de Pythagore, qui stipule que dans un triangle rectangle, la somme des carrés des longueurs des côtés adjacents à l’angle droit est égale au carré de la longueur de l’hypoténuse. Cette vérification aide à comprendre et à appliquer correctement les formules de volume.
Le calcul du volume d’un triangle rectangle repose sur l’aire de sa base et sa hauteur. En regroupant ces notions fondamentales, de nombreuses applications pratiques se présentent, soulignant l’importance de maîtriser ces concepts en géométrie. Actuellement, les entreprises et les professionnels exploitent également les principes du volume dans divers domaines, comme la mode, avec des tendances actuelles, ou des études exploratoires en intégrant les volumes dans leur logique de conception.
Enfin, pour des connaissances actualisées et plus approfondies, explorer les tendances et innovations s’avère enrichissant.
| Méthode de calcul | Applications pratiques |
| Aire du triangle : A = (b × h) / 2 | Calcul de surface pour l’architecture et la construction. |
| Volume d’un prisme triangulaire : V = A × hauteur | Utilisé dans la fabrication de pièces industrielles. |
| Utilisation de la hauteur des triangles rectangles | Indispensable pour le design de toits inclinés. |
| Démonstration du caractère rectangle : Théorème de Pythagore | Analyse géométrique dans l’ingénierie. |
| Calcul via les longueurs des côtés | Optimisation dans les sports et les loisirs de plein air. |
Le calcul du volume d’un triangle rectangle est un sujet essentiel dans le domaine des mathématiques appliquées. En effet, comprendre comment déterminer le volume d’une figure en trois dimensions à partir de ses dimensions de base est crucial dans divers domaines tels que l’architecture, l’ingénierie et même la modélisation 3D. Cet article vise à simplifier ce concept en présentant une méthode claire et des applications pratiques.
Définition du volume d’un solide
Le volume représente la mesure de l’espace occupé à l’intérieur d’un solide. Pour un prisme triangulaire, dont fait partie le triangle rectangle, le volume peut être calculé en multipliant l’aire de la base par la hauteur du prisme. Ce concept de volume est également essentiel pour saisir comment les objets prennent de l’espace dans le monde réel.
Calculer l’aire d’un triangle rectangle
Avant de pouvoir calculer le volume d’un triangle rectangle, il est nécessaire de déterminer son aire. L’aire A d’un triangle rectangle peut se calculer avec la formule suivante :
A = (b × h) / 2
où b est la base et h est la hauteur, soit les deux côtés qui se rencontrent à angle droit. Cette formule simple vous permettra d’obtenir l’aire rapidement et est essentielle pour le calcul du volume subséquent.
Formule pour le volume d’un prisme triangulaire
Une fois l’aire de la base calculée, il est temps de déterminer le volume. Pour un prisme triangulaire, le volume V peut être calculé avec la formule :
V = A × H
où A est l’aire de la base (triangle rectangle) et H est la hauteur du prisme. Par exemple, si l’aire d’un triangle rectangle est de 20 cm² et que la hauteur du prisme est de 10 cm, le volume sera :
- V = 20 cm² × 10 cm = 200 cm³
Applications pratiques du calcul de volume
La maîtrise du calcul du volume d’un prisme triangulaire a des applications concrètes dans plusieurs domaines. Dans l’architecture, par exemple, ces calculs aident à concevoir des structures en prévoyant leurs dimensions et leur capacité à contenir des matériaux. En ingénierie, savoir comment estimer le volume peut influencer la conception de réservoirs ou de contenants adaptés aux produits chimiques. Enfin, dans le domaine de l’animation 3D, ces concepts sont fondamentaux pour la modélisation et la simulation de solides.
Pour ceux qui souhaiteraient approfondir leur apprentissage des tendances de mode et les innovations qui influencent le style individuel, découvrez les dernières recommandations et astuces sur les incontournables du dressing parisien, ou explorez comment rester chic tout au long de l’année sur les tendances de 2021 ainsi que des conseils sur l’influence de la coiffure sur votre style.
- Méthode de calcul
- Volume = Aire de la base × Hauteur
- Aire de la base (triangle rectangle) = (Base × Hauteur) / 2
- Hauteur du prisme = distance entre les bases
- Volume = Aire de la base × Hauteur
- Aire de la base (triangle rectangle) = (Base × Hauteur) / 2
- Hauteur du prisme = distance entre les bases
- Applications pratiques
- Construction de structures géométriques
- Modélisation de volumes en architecture
- Calcul de matériaux nécessaires pour une construction
- Construction de structures géométriques
- Modélisation de volumes en architecture
- Calcul de matériaux nécessaires pour une construction
- Exemples concrets
- Volume d’un prisme triangulaire dans un bâtiment
- Évaluation de la capacité d’un réservoir en forme de pyramide triangulaire
- Calcul de l’espace utilisé dans un modèle en 3D
- Volume d’un prisme triangulaire dans un bâtiment
- Évaluation de la capacité d’un réservoir en forme de pyramide triangulaire
- Calcul de l’espace utilisé dans un modèle en 3D
- Importance du volume
- Détermination de la capacité de stockage
- Optimisation des espaces dans l’urbanisme
- Analyse des proportions dans des œuvres artistiques
- Détermination de la capacité de stockage
- Optimisation des espaces dans l’urbanisme
- Analyse des proportions dans des œuvres artistiques
- Volume = Aire de la base × Hauteur
- Aire de la base (triangle rectangle) = (Base × Hauteur) / 2
- Hauteur du prisme = distance entre les bases
- Construction de structures géométriques
- Modélisation de volumes en architecture
- Calcul de matériaux nécessaires pour une construction
- Volume d’un prisme triangulaire dans un bâtiment
- Évaluation de la capacité d’un réservoir en forme de pyramide triangulaire
- Calcul de l’espace utilisé dans un modèle en 3D
- Détermination de la capacité de stockage
- Optimisation des espaces dans l’urbanisme
- Analyse des proportions dans des œuvres artistiques
Introduction au volume d’un triangle rectangle
Le calcul du volume d’un triangle rectangle peut sembler complexe, mais en réalité, en comprenant les concepts de base, il devient accessible à tous. Ce guide vous propose une méthode claire pour calculer ce volume, ainsi que des applications pratiques pour mieux visualiser et utiliser ces notions en mathématiques. Nous aborderons d’abord les éléments fondamentaux tels que l’aire d’un triangle rectangle et ensuite nous verrons comment utiliser cette aire dans le cadre de différentes applications géométriques.
Comprendre l’aire d’un triangle rectangle
La base du calcul du volume d’un triangle rectangle repose sur la capacité à déterminer son aire. Un triangle rectangle se caractérise par un angle droit, et ses côtés adjacents à cet angle sont appelés cathètes. Pour trouver l’aire (A) de ce triangle, on utilise la formule :
A = (b × h) / 2
où b représente la longueur de la base et h la hauteur, c’est-à-dire la longueur du côté perpendiculaire à la base. Cette formule vous permet de calculer rapidement l’aire de tout triangle rectangle, ce qui est une étape cruciale avant de passer au calcul du volume.
Calcul du volume d’un triangle rectangle
Une fois que vous avez calculé l’aire du triangle rectangle, vous pouvez passer au calcul du volume, mais d’abord, il faut bien préciser que le volume se réfère au contenu d’un solide. Pour un prisme triangulaire dont la base est un triangle rectangle, la formule pour calculer le volume (V) est :
V = A × h
Dans cette formule, A représente l’aire de la base que nous avons calculée précédemment, tandis que h désigne la hauteur du prisme, c’est-à-dire la distance entre les deux bases. En multipliant l’aire de la base par la hauteur, vous obtiendrez le volume du prisme triangulaire.
Exemple de calcul pratique
Pour illustrer, prenons un triangle rectangle dont les longueurs des cathètes sont respectivement 6 cm et 8 cm. Calculons d’abord l’aire :
A = (6 × 8) / 2 = 24 cm²
Si nous avons un prisme dont la hauteur est de 10 cm, le calcul du volume serait :
V = 24 × 10 = 240 cm³
Ce calcul montre clairement comment les dimensions d’un triangle rectangle, combinées à sa hauteur, peuvent produire un volume significatif.
Applications pratiques du calcul de volume
Connaître le volume d’un triangle rectangle et les prismes qui en découlent a plusieurs applications pratiques dans la vie quotidienne et dans divers domaines scientifiques. Par exemple, en ingénierie, cette connaissance aide à concevoir des structures solides et efficaces, tout en optimisant les matériaux utilisés. Dans le domaine de l’architecture, le volume est essentiel pour la planification de l’espace et l’estimation des matériaux nécessaires.
Dans un contexte éducatif, la compréhension du volume permet aux étudiants de mieux appréhender les concepts de la géométrie et de renforcer leurs compétences en résolution de problèmes. À travers des exercices pratiques, ils apprennent à appliquer ces concepts dans des situations réelles, augmentant ainsi leur confiance et compétence en mathématiques.
Conclusion sur les volumes et leurs calculs
La méthode de calcul du volume d’un triangle rectangle est non seulement simple mais également riche en applications. En maîtrisant les étapes pour calculer l’aire et en appliquant cette connaissance à la hauteur d’un prisme, il est possible de résoudre une variété de problèmes géométriques. Cet apprentissage ouvre des portes vers une compréhension plus approfondie de la géométrie et de ses applications réelles.